Lecture # 1: Understanding the Concept of Digital Memory
The beauty of the NAND gates can be seen more closely by observing the connection below. This kind of feedback system had made the invention of digital memory system becomes remarkable and realistic with respect to the history of human-machine interaction.
And a simple example of input and output signals is demonstrated below as to enhance your understanding.
As usual, a simple example may be a good feed for all J.
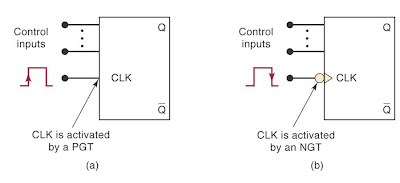
A typical clock wave is depicted in figure below. Understand the PGT and NGT as described by the lecturer J.
The flip-flop is clever enough to understand which transition should be chosen because of the help of the edge detector circuit as shown below.
Now, let’s apply the CLK to the SR latch. In this case, conventionally, we call it Clocked S-R Flip-flop.
And also apply the CLK to the gated D latch (EN), which is can be called as Clocked D Flip-flop.
It is forgivable situationJ if the students are not interested to understand more on the behavioral of this circuit at this moment. Let’s focus straight to the point where the outcome of the circuit is as shown below.
Having gone through the note and lecture, what is the weakness of the circuit? Surely the answer is the ‘invalid state’! As told by the lecturer J.
One of the ways to compensate the problem is as shown below with the invention of so called D latch.
As usual, a simple example may be a good feed for all J.
So, what is the weakness or drawback that can be seen from D latch? Very good! Even though it solved the problem of invalid state, but it has limited the input capability to only ‘D’ input. However, this kind of data operation still useful in the application of data storage or delay (as the name implies).
Alternatively, the NOR latch as shown below also produces and reveal the meaning of digital memory. You should by now, understand the ‘No change’ state where the data is held by the system. The term ‘lock’, ‘hold’, ‘still’ or ‘latch’ can be used to represent the meaning of data memory in this early understanding of the digital memory concept.
Before we proceed further, let us try to make the system work better by understanding the function of CLOCK (CLK) in which we would like to have the whole scenario as:
“Change the output state ONLY when instructed to do so”
A typical clock wave is depicted in figure below. Understand the PGT and NGT as described by the lecturer J.
The flip-flop is clever enough to understand which transition should be chosen because of the help of the edge detector circuit as shown below.
Now, let’s apply the CLK to the SR latch. In this case, conventionally, we call it Clocked S-R Flip-flop.
And also apply the CLK to the gated D latch (EN), which is can be called as Clocked D Flip-flop.
The weakness in SR flip-flop remains unchanged if we can’t settle the problem of ‘invalid state’ more wisely! The invention of D flip-flop, however had contributed some efforts whereby the invalid state is discarded, but reduced some other advantages of the flip-flop.
The best solution is the invention of J-K flip-flop! Figure below shows the additional wiring for gated S-R latch with the insertion of clock (CLK) and edge detector.
It is forgivable situationJ if the students are not interested to understand more on the behavioral of this circuit at this moment. Let’s focus straight to the point where the outcome of the circuit is as shown below.
What is the beauty of the story? Observe again the last example shown for the J-K flip-flop !!
Now, we have a good instrument to pursue the invention of digital memory and other important application.
Ref: Digital Systems i.e Thanks to Bro Ronald J. Tocci for the images used and facts, of course :)
Next lecture:
Ref: Digital Systems i.e Thanks to Bro Ronald J. Tocci for the images used and facts, of course :)
Next lecture:
- The counter.
- The frequency divider.
Lecture # 2: Application of J-K and D Flip-Flop
Lecture # 2:
Suppose we have 2 J-K flip-flop connected as asynchronous or ripple, in such a way that the outputs are always ‘TOGGLE’ ! This can be done by setting all Js and Ks at HIGH level as shown below.
The clock is given to the first f/f where the output, A becomes a clock to the second f/f and produce output B. Both are negative triggered.
Observe the outputs’ signals. If the given CLK is 4 Hz (4 period per second), notice that the o/p, A receives 2 Hz while o/p, B end up with 1 Hz.
What does this imply?... Brilliant! Wowowwow… it’s counting and dividing the frequency!
Taking B as MSB and A as LSB, we have:
00, 01, 10 and 11 followed by 00, 01, 10,11,00,01,…. Continuously if the CLK continuously supplied and J-K are always HIGH.
What is the outcome of the circuit if we connect one or two more J-K f/f as shown below?
It counts from ‘0’ to ‘15’. Simply we can derive a formulae as:
Total numbers to be counted is 2N , where N = number of f/f.
The counting includes ‘0’. In the case of 4 f/fs, we have 16 states including ‘0’.
So, we have done thus far:
1 f/f, we count 0,1,0,1,…
2 f/f, we count 0,1,2,3,0,1,2,3,…..
3 f/f, we count 0,1,2,3,4,5,6,7,0,1,2,3,4,5,6,7,0,1,2,…
4 f/fs, we count 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0,1,2,3,…
That is good as a start in designing the counter! But, what is the limitation of this kind of connection?
Recall Grade 1 Primary School! J
You should also know how to count the sequence pattern such as below.
0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, ……. (the last digit in sequence is depends on what you want it to be! This will conflict with 2N !!)
Or
3, 4, 5, 6, 3, 4, 5, 6, ….. (Start and ending the counting whichever you like!)
Or
2,4,6,8,10,…..
3,6,9,12,15,….
And many more as what you have done for ‘multiplication table’.
Or,
9,8,7,6,5,4,3,2,1,0…. (Counting down)
Before we proceed further, let me introduce “Asynchronous Preset and Clear Inputs”.
Study the figure below.
Figure 2.1
Both preset and clear inputs can be seen as active low and ‘mandatory’ J. i.e. which means, if the ‘preset’ input is injected with ‘0’ input, the output of J-K flip-flop is forced to go ‘HIGH’. If the ‘clear’ input is given ‘0’ input, the output is forced to go ‘LOW’ (clear or reset or zero). Understand the truth table !
Now, we have almost a completed tools to design a counter whichever we like!.
Study the examples below and ask lecturer in the class for any doubt!
MOD-6
(a) MOD-14 and (b) MOD-10 (decade counter)
Counting down Counter
There are a number of ICs available in the market for designing the counter.
Study these ICs and will be discussed in the class.
Examples of IC ASYN. (Ripple) Counter:
- 74293
- 7493
- 7490
Notes: Hand-outs will be distributed in the class. :)